Follow this link to skip to the main content
Image of a Lunar Base base.
Button that takes you to the Overview Section. Image that says Teacher's Toolkit. Button that takes you to the Student Materials Section. Button that takes you to the Mission Day Section.
 Teacher's Toolkit

Home
Scope and Sequence
Lesson Plans

Introduction
Math Activities
Pre-Mission Preparation
Mission

Your "To-Do" List
Resources

 Lesson Plan 4: Probability

Introduction
In the Target Moon mission NASA will need to determine the likelihood of a comet hitting three lunar settlements. NASA must find the probability that the settlements will be hit by the comet to decide whether the astronauts and resources at each site should be evacuated. Probability is the likelihood that a certain outcome will take place. Probability is calculated by creating a ratio of the number of ways an event can happen to the total number of possible outcomes and can be shown as a fraction, decimal, or percentage.

Duration

30-45 minutes

Vocabulary

outcomes: possible results in a situation.

event:  the particular outcome that you are looking for.

probability: a ratio of the number of ways an event can happen to the total number of possible outcomes.

Pi (π): for any circle the ratio of the circumference to the diameter; π equals 3.14.

NCTM Standards for Mathematics

Grades 6-8; Data Analysis and Probability

Understand and apply basic concepts of probability.

  • Use proportionality and a basic understanding of probability to make and test conjectures about the results of experiments and simulations.

Materials

  • Copies of Student Worksheet: Probability for each student

  • Pencils

Formulas to Review

Area of a Circle = π   ×   r2

Area of a Square or Rectangle = length   ×   width

Procedure

  1. Decide how you want the students to work on the activity. You may choose to have the students work individually or in cooperative groups. Another option would be to assign this activity for homework and review the answers together in class.
  2. Discuss all vocabulary in the lesson, including ratio, rate, proportion, and cross-multiplication.
  3. Preview the activity with the students. Read the student version of the instructions out loud in class. Allow time for questions and discussion.
  4. Make sure that your students understand the relevance of this activity to their mission work. During the Target Moon live simulation students will calculate probability to determine the likelihood that the comet will hit the three lunar settlements.

Example Problem
If you flip a token onto this game board, what is the probability that your token will land on the circle?

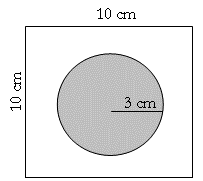
Image of a circle (r=3cm) in a box that is 10cm by 10cm.

To find the probability that the token will fall within the circle on the game board, you need to find the area of the circle and the total area of the game board.  Once you have both areas, you should divide the area of the circle by the total area of the game board to find the probability.  Use the following formula:

Probability (of landing in the circle) =             area of circle_                    
                                                                total area of the game board

In this problem the game board is a square shape, so the formula for the area of a square is used to find the total area of the game board.

       π   ×   r2
= ______________
    length × width

       3.14   ×   3cm  ×   3cm
= _________________________
               10cm × 10cm

       28.26 cm2
= ______________
          100cm2

≈ 0.28, or 28%

The probability that the coin will land in the circle is approximately 28 percent.

Probability Practice
Complete the following probability problems using the example problem to guide you.  Write your answer as a percentage.

  1. Look at the following game board.  If you toss a coin onto the game board, what is the probability that you will land on a square that contains a triangle? 

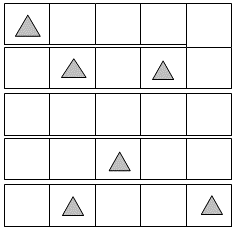
Image of 5 x 5 table with triangles in various locations.

                                                                                                6 square units
Probability of landing on a square with a triangle = __________________
                                                                                              25 square units

                                                                          = .24, or 24 percent

  1. Geoff likes to play darts.  If he throws a dart at the board, what is the probability that he will hit a bull’s-eye?

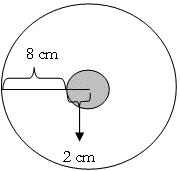
Image of a circle with a bullseye with full circle radius of 8cm and bullseye radius of 2cm.

 

                                                             area of bull's-eye
Probability of getting a bull's-eye = ___________________________
                                                            area of entire dartboard

                                                             π   × 2cm × 2cm
                                                     = ______________________
                                                             π   × 10cm × 10cm

                                                                          12.56 cm2
                                                                  = ______________________
                                                                         314cm2

= .04, or 4 percent

  1. A resort is planning to dig a well to aid in the watering of its prize flower garden.  Here is a diagram of the garden.    

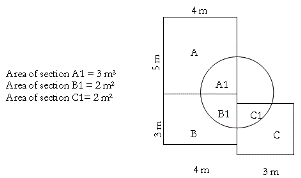
Image showing a diagram of a garden.

Garden A is a rose garden, garden B contains tulips, and garden C contains lilies. The well will be placed somewhere within the circle. What is the probability that the well will be dug in the rose garden? In the tulip garden? In the lily garden? 

                                                                                                                    area of section A1
Probability that the well will be placed in the rose garden = ___________________________
                                                                                                                total area of rose garden

                                                             3m2 (insert from chart)
                                                     = ________________________________
                                                             5m × 4m

                                                                          3m2
                                                                  = ______________________
                                                                         20m2

                                                                                    =          .15, or 15 percent            

Solve problems for tulip garden and lily garden using the same formula and plugging in the values from the chart and diagram.      

Probability that the well will be placed in the tulip garden     ≈          .17, or 17 percent

Probability that the well will be placed in the lily garden        ≈          .22, or 22 percent

Analysis Questions

Answer the following questions based on the probability problems you have solved. 

  1. Can you give an example of where probability is used in your daily life?

Possible examples include forecasting weather, calculating the odds of winning the lottery or a game of roulette, insurance company rates, health care statistics, etc.

  1. How can probability help you to make decisions?  Give an example?

Probability can help you make an informed decision in a situation where more than one outcome can result.  For example, if there is a 80 percent chance that it will snow on a day that you are scheduled to travel, you may postpone your trip.
Animation showing all of the innovative programs for digital learning that the Center for Educational Technologies has developed. Some of them include: EVA Alert, M.A.R.S., and Target Moon.

The Center for Educational Technologies® at WJU has developed a series of innovative programs for digital learning. These programs provide teachers with an all-inclusive package comprised of curriculum aligned with state and national standards and a live “mission” via technology. The programs were designed around best practice models and principles derived from the latest educational research.

 Button that takes you to the Classroom of the Future home page. The caption reads: Developed by the NASA-Sponsored Classroom of the Future TM.
Image that shows the bottom border of the page.
© 2005-2006 by Wheeling Jesuit University/Center for Educational Technologies®. 316 Washington Ave., Wheeling, WV, 26003-6243. Target Moon was developed under a cooperative agreement with NASA. All rights reserved. Privacy Policy and Terms of Use.
Image of Live Simulation Target Moon Logo that links to the home page.